This blog-post is the first of a short serie on Multi-Agent control and RL. The objective here is to cover the different models of multi-agent interactions, from repeated matrix games to partially observable Markov games. Going up the game hierarchy (from less to more general) we will detail what constitutes valid policies and how they differ from their usual fully and partially observed MDPs cousin.

We focus below on so-called normal-form games: both players play at the same time. Games that unroll in a turn-based fashion are called extensive-form games. The difference may seem thin, but deeply impacts the potential solution concepts. For instance, once can find deterministic optimal policies in some extensive form games since the opponent’s move is perfectly known. In normal-form games, some level of randomness is often required to prevent the opponent from guessing our moves.

Agent Objectives

Before diving into a game classification based on agents’ observation models, let’s discuss the different possibilities when it comes to the agents’ objectives. As in a classical MDP, those will be materialised via rewards functions— for concreteness, we will denote them $r^1, \ldots, r^n$ for a game with $n$ agents. In all generality, there exists no built-in relationship between said rewards. This is a general-sum game. Such a game admits two important sub-games:

• In a zero-sum games describe games, agents have opposite objectives and act competitively. Formally, the agents rewards sum to zero at each round of the game: $$ \sum_{i=1}^n r_t^i = 0, \quad \forall t\geq 1\; . $$ Perhaps the most common instance of such a game is the two-player zero-sum game, where $r_t^1 = -r_t^2$.
• Cooperative games (a.k.a team-games or common-reward games) designate settings where the agents share the same objective and act in a fully cooperative fashion. Formally, this means that at any round $t$: $$ r_t^1 = \ldots = r_t^n \; . $$

All instances of this game classification can be coupled with the following one, concerned with observations rather than rewards.

Agent Observations and Interactions

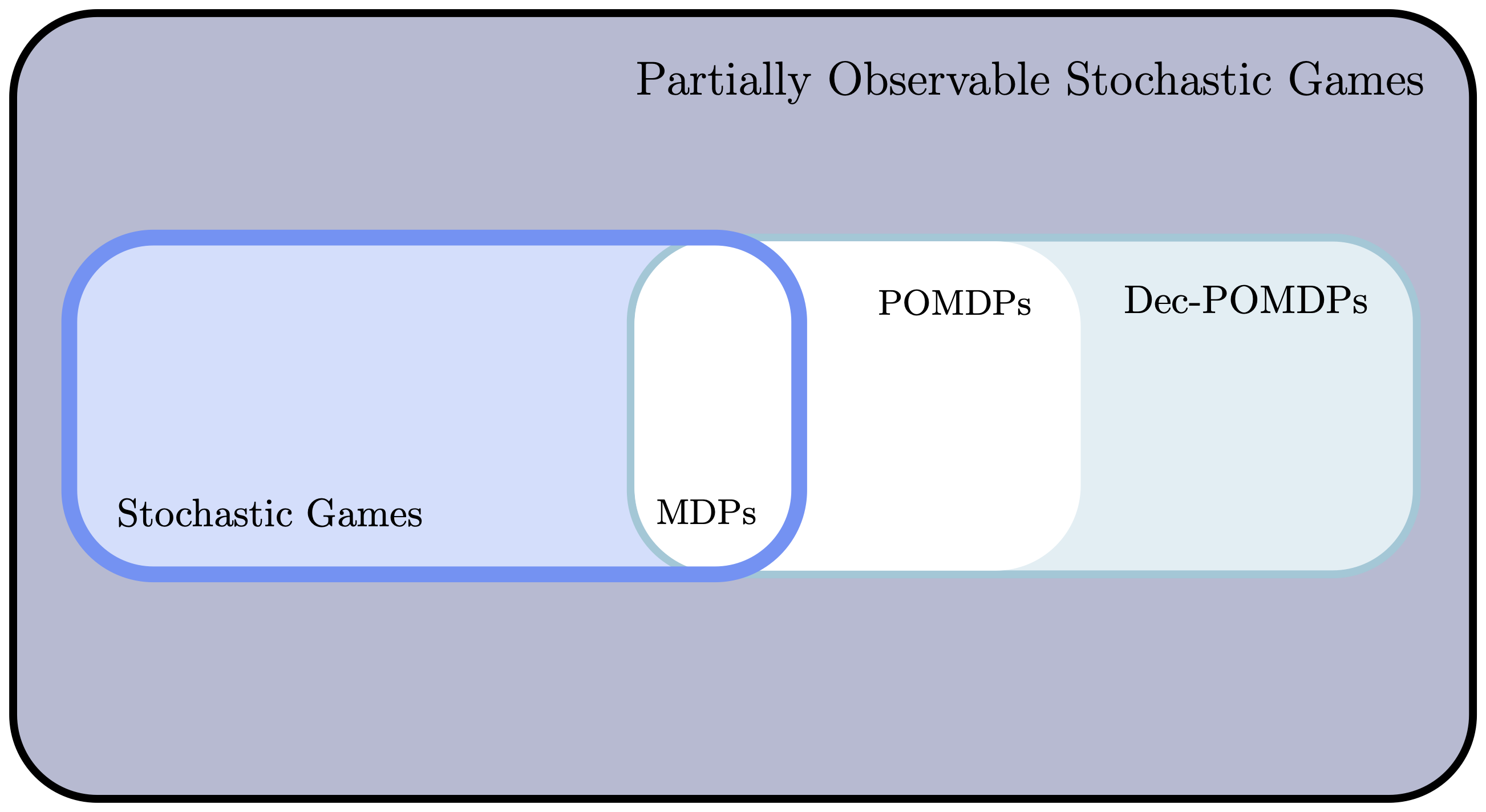
Another important classification of games concerns the level of information accessible to the agents, as well as their actions’ impact on their environment. Below, we go up the hierarchy of multi-agents settings, from less to more general. This hierarchy evolves with the multi-agents’ environment dynamic, their knowledge of each other and of the game’s hidden state (if any).

Repeated Matrix Games

A matrix game can be represented via its number of player $n\in\mathbb{N}$, a combination of its agent action space: $$\mathcal{A}=\mathcal{A}_1\times\ldots\times\mathcal{A}_n\;,$$ as well as a collection $\bm{r} = (r^1, \ldots, r^n)$ of reward functions, each mapping $\mathcal{A}$ to $\mathbb{R}$. There is no notion of state; the agents’ actions do not impact the environment in any way.

A repeated matrix game simply is the repetition of the same matrix game for $T\in\mathbb{N}\cup\{+\infty\}$ rounds.

This is a perfect knowledge game; each agent has access to the others’ previous actions. At each round $t$, each agent can base its decision $a_t^i$ based on the game’s full history $\bm{h}_{t-1}$. A valid decision rule $d_t^{\,i}$ for agent $i$ therefore maps said history to a distribution over $\mathcal{A}_i$. A collection of agent decision-rules form the marginal policy $\pi^i = (d_1^{\,i}, d_2^{\,i}, \ldots)$. The joint policy is: $$\bm{\pi} = (\pi^1, \ldots ,\pi^n)\; .$$

Stochastic Games

Up the game hierarchy lie stochastic games (a.k.a Markov games) where the agents’ actions now influence the environment’s state, which lives in some set $\mathcal{S}$. The definition extends the classical MDP definitions to handle several agents, by having the transition kernel now depends on the joint action: $$ \begin{aligned} p(\cdot \vert s, \bm{a}) &= \mathbb{P}(s_{t+1}=\cdot \vert s_t=s, \bm{a}_t = a)\\ &= \mathbb{P}(s_{t+1}=\cdot \vert s_t=s, a_t^1=a^1, \ldots, a_t^n = a^n)\;. \end{aligned} $$ The reward functions now map $\mathcal{S}\times\mathcal{A}$ to $\mathbb{R}$.

The agents are still fully aware of the environment and of each other. Namely, they observe the joint action and can base their policy on the whole game history, along with the current state. In other words, at round $t$ a valid decision-rule for some agent will be: $$ \begin{aligned} d_t^{\, i} : (\mathcal{S}\times\mathcal{A})^{t-1}\times\mathcal{S} &\mapsto \Delta(\mathcal{A})\; ,\\ \bm{h}_{t-1}, s_t &\mapsto d_t^{, i}(\bm{h}_{t-1}, s_t) \; . \end{aligned} $$

Partially Observable Stochastic Games

Partially observable stochastic games (POSGs) are the most general form of normal form games, and extend the notion of POMDPs to multi-agent setting. The additional ingredients to go from a stochastic game to a partially observable stochastic game are (1) a combinatorial observation space $\Omega = \Omega_1\times\ldots\times\Omega_n$ and (2) an observation kernel $q(\cdot \vert s, \bm{a})$ defined as: $$ q(\bm{\omega} \vert s, \bm{a}) = \mathbb{P}\left(\bm{\omega}_t = \bm{\omega} \vert s_t = s, \bm{a}_{t-1}=\bm{a} \right) ,\quad \forall\bm{\omega} = (\omega^1, \ldots, \omega^n)\in\Omega\; . $$

The particularity of POSGs is that agents can neither observe the state $s_t$ (similarly to a POMDP), but neither can they access other agents’ observations and past actions. Strategies must therefore be decentralised. Formally, this means that a decision rule for a given agent only ingests said agent history $h_t^i = (\omega_1^i, a_1^i, \ldots, a_{t-1}^i, \omega_t^i)$. In other words, a valid decision-rule at round $t$ is: $$ d_t^i : (\Omega_i\times\mathcal{A}_i)^t \times \Omega_i \mapsto \Delta(\mathcal{A}_i)\; . $$

Communications

Despite such a decentralised scenario, agents need not be utterly blind to each others. For instance, the joint observation space $\Omega$ can explicitly include communication channels, on which agents will exchange information (this degree of freedom is then included in the joint action space $\mathcal{A}$). Agents can also develop implicit communications; information regarding some agent $j$ (e.g. its position) can be available to agent $i$ via its observations $\omega_i$. As such, agent $j$ can pass implicit signals to agent $i$ (e.g., by having its position jitter). Given the obligation for decentralised policies, learning such coordination and communication mechanisms is one of the main challenges when it comes to solving POSGs.

Decentralised POMDPs

Cooperative POSGs are called Decentralised POMDPs. In this setting, one needs to control a coalition of agents pursuing a common goal $r$, but with limited observations about their environment and each others.

Dec-POMDPs have arguably been one of the main centres of interest in the Multi-Agent RL community. Indeed, the cooperative nature of such games (agents are optimising a common reward) removes the need for more ambiguous game-theoretic objectives. This allows one to focus on the development of algorithms that allows emergent coordination and communication mechanisms between agents. This cannot be done by direct extension of pure POMDPs (which is a Dec-POMDP with $n=1$). Indeed, the necessity of deploying decentralised policies clashes with typical control methods for POMDPs; for instance, an agent-wise belief can no longer be computed (at least not without some approximations).

Resources

This blog post’s material is inspired from [Shoham and Leyton-Brown] and the Multi-Agent RL book.