This post is interested in state estimation in HMMs: filtering, prediction and smoothing. We will introduce state estimation as the solution of an optimisation problem, and prove the celebrated recursive updates for each inference use-case. A special attention will be given to HMM filters (and how they easily generalise to the celebrated Kalman filters).

Hidden Markov Models

We study Hidden Markov Models (HMMs): partially observable processes formalised by a tuple $(\mathcal{X}, \mathcal{Y}, p, q)$. $\mathcal{X}$ is the state-space and $\mathcal{Y}$ the observation space. The distribution $p$ materialises the stochastic process for the state $x_t\in\mathcal{X}$, which be observed via observations $y_t\in\mathcal{Y}$. $$ \left\{\begin{aligned} x_{t+1} &\sim p(\cdot \vert x_t) \;, \\ y_{t+1} &\sim q(\cdot \vert x_{t+1}) \;. \end{aligned}\right. $$

HMMs come with strong Markovian structure (see Fig. 1). In particular, we have the following identities: $$ \begin{aligned} p(x_t \, \vert \, x_{1}, \ldots x_{t-1}) &= p(x_t \, \vert \, x_{t-1}) \;,\\ p(y_t \, \vert \, x_{1}, \ldots x_{t-1}) &= p(y_t \,\vert \, x_t)\; . \end{aligned} $$

Given the finite nature of the problem, it can be useful to adopt vectorial notations. Let $n=\vert \mathcal{X}\vert$ and $m=\vert \mathcal{Y}\vert$. Below, bold notations refer to matrices and vectors. For instance, if $\pi$ is a distribution over $\mathcal{X}$ we denote $\boldsymbol{\pi} := (\pi_{x_1}, \ldots, \pi_{x_n})^\top\in\mathbb{R}^{n}$. Similarly, we will use the matrix notation $\mathbf{P}\in\mathbb{R}^{n\times n}$ and $\mathbf{Q}\in\mathbb{R}^{n\times m}$ for: $$ \begin{aligned} [\mathbf{P}]_{xx^\prime} = p(x^\prime\vert x)\;,\\ [\mathbf{Q}]_{xy} = q(y\vert x)\;. \end{aligned} $$

Optimality

We are concerned with state estimation: building estimate $\hat{x}_{t\vert n}$ of the state $x_t$, given a set of contiguous observations $\{y_{1:n}\}$. The actual value of $n$ allows us to separate several uses cases:

1. $t=n$ is filtering: producing an estimate of the current state given all observations collected so far,
2. $t>n$ is predicting: estimating the future value of the state given all observations collected so far,
3. $t<n$ is smoothing: estimating the current value of the state given all observations (future and past).

We are interested in estimators minimising a squared error criterion. In the rest of this section, we will make this explicit for filtering. It naturally extends to the other set-up. In optimal filtering, we compute: $$ \tag{1} \hat{x}_{t\vert t} \in \argmin_{x} \mathbb{E}\left[(x-x_t)^2 \, \middle\vert\, y_{1:t}\right]\; . $$

Such an estimator has the good taste of admitting a closed-form: $$ \begin{aligned} \tag{2} \hat{x}_{t\vert t} &= \mathbb{E}\left[x_t \,\middle\vert\, y_{1:t}\right]\;.\\ &= \sum_{x\in\mathcal{X}} x \cdot p(x_t=x\vert y_{1:t})\; . \end{aligned} $$

Thanks to the smoothing property of expectation, it is also unbiased. Further, it is quite clear that to compute this estimator, one should first compute the conditional $p(\cdot\vert y_{1:t})$.

Bregman-divergences

The $\ell_2$-norm is sometimes a clumsy way to measure distance between states. For instance, one usually prefers distributional distances, e.g. the Kullback-Leibler divergence if the state lives in a simplex. The good news is that the estimator from (2) is also the solution of the following program, where the discrepancy to $x_t$ is measured by any Bregman divergence! Formally, for any differentiable and convex function $f:\mathcal{X}\mapsto\mathbb{R}$, denote $D_f : \mathcal{X}\times\mathcal{X}\mapsto\mathbb{R}$ the associated Bregman divergence: $$ D_f(x\, | \, x^\prime) := f(x) - f(x^\prime) - f^\prime(x^\prime)(x-x^\prime)\;. $$ Then, we have that $\hat{x}_{t\vert t}$ is also the solution to: $$ \hat{x}_{t\vert t} \in \argmin_{x} \mathbb{E}\left[D_f(x_t\, | \, x) \middle\vert y_{1:t}\right]\;. $$

Filtering

We saw in the previous section that the filtering problem boiled down to computing the conditional $$ \pi_{t}(\cdot) := p(x_t=\cdot\vert y_{1:t})\;. $$ Sounds tedious. But we are in luck: it actually follows a nice recursive structure.

(3) can be written in vectorial form: $$ \boldsymbol{\pi}_t \propto \text{diag}(\mathbf{Q}_{y_t})\mathbf{P}^\top\boldsymbol{\pi}_{t-1}\; , $$ where $\mathbf{Q}_{y_t}$ is the $y_t$ line of $\mathbf{Q}$. Concretely, this means that one can compute $\pi_t$ recursively, by incorporating the observations $\{y_{1:t}\}_t$ one at a time. The update rule (3) is sometimes decomposed into two steps:

1. Prediction computes $\pi_{t\vert t-1}$, the state distribution after the HMM steps before the observation is emitted: $$ \pi_{t\vert t-1}(x) = \sum_{x^\prime\in \mathcal{X}} p(x\vert x^\prime)\pi_{t-1}(x^\prime)\; . $$
2. Measurement incorporates the knowledge of $y_t$: $$ \tag{4} \pi_t(x) \propto p(y_t\vert x) \pi_{t\vert t-1}(x)\; . $$

Beyond HMMs

The ideas presented above are easily generalised to continuous states and observations spaces. Representing the different probability measures by their densities, one can write: $$ \pi_t(x) \propto p(y_t\vert x_t) \int_{\mathbb{R}} p(x\vert x^\prime)\pi_{t-1}(x^\prime) dx^\prime\; . $$ The usual difficulty arises when this update step does not admit a closed form (which is basically almost always), and the resulting $\pi_t$ does not have to belong to a parametric distribution (e.g. Gaussian). The well-known exception to this rule arise when $\pi_{t-1}$ is a normal distribution, and both the transition and emission kernels are also normal. Then (4) admits an explicit form and $\pi_t$ is also Gaussian. This is the setting of the celebrated Kalman filter—which is often presented via the prediction and measurement framework we discussed above.

Prediction

This will be a short section: the main steps for completing predictions were already covered in the previous section. For filtering, the prediction step computes: $$ \pi_{t+1\vert t}(x) = \sum_{x^\prime\in \mathcal{X}} p(x\vert x^\prime)\pi_{t}(x^\prime)\; . $$ This can be iterated a few times to compute $\pi_{t+k\vert t}$.

Smoothing

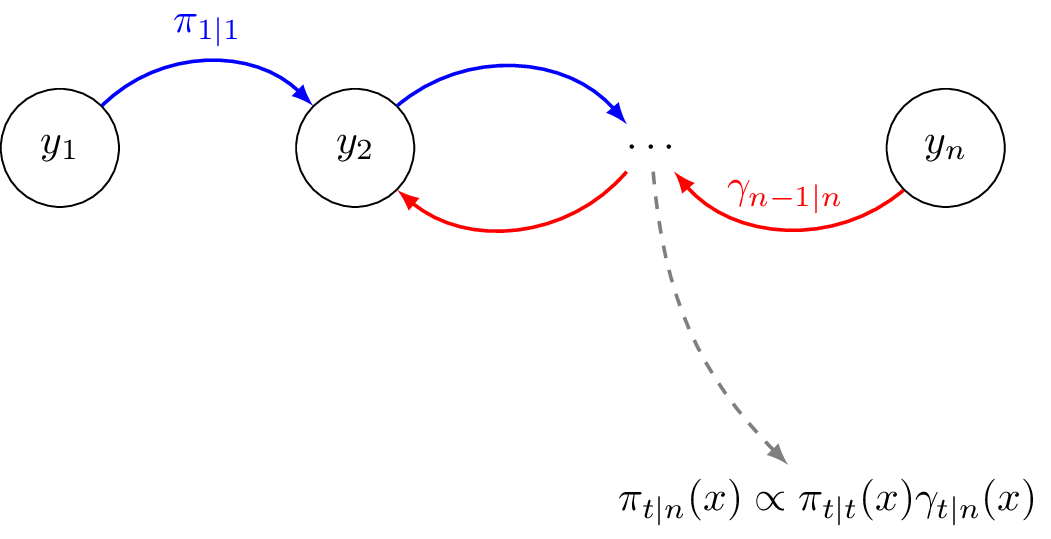
Smoothing actually covers several concrete use cases (fixed-point, fixed-lag, fixed-interval). Below, we are interested in the fixed-interval setting. Let $n$ be fixed; we wish to estimate $\pi_{t\vert n}$ for every $t=1, \ldots, n$ given $y_{1:n}$. Concretely, we wish to compute all the conditionals $p(x_t\vert y_{1:n})$. Observe that: $$ \begin{aligned} p(x_t\vert y_{1:n}) &\propto p(x_t, y_{t+1:n} \vert y_{1:t})\;, &(\text{Bayes rule}) \\ &= p(y_{t+1:n}\vert x_t, y_{1:t}) p(x_t\vert y_{1:t})\;,\\ &= p(y_{t+1:n}\vert x_t)p(x_t\vert y_{1:t})\;, \end{aligned} $$ which, by denoting $\gamma_{t\vert n}(x) = p(y_{t+1:n}\vert x_t=x)$ we will write:

Another good news: $\gamma_{t\vert n}$ also checks a recursive update rule.For any $x\in\mathcal{X}$: $$ \gamma_{t\vert n}(x) = \sum_{x^\prime\in\mathcal{X}} q(y_{t+1}\vert x^\prime)p(x^\prime\vert x)\gamma_{t+1\vert n}(x^\prime)\;. $$ It can therefore be efficiently computed via backward recursion in time, starting from $\gamma_{n\vert n}\equiv 1$. In vectorial notations, it writes: $$ \boldsymbol{\gamma}_{t\vert n} = \mathbf{P}\text{diag}({\mathbf{B}}_{y_{t+1}})\boldsymbol{\gamma}_{t+1\vert n}\;. $$

Going back to smoothing, we now understand it can be achieved by a forward / backward algorithm. A first forward loop returns the filtering estimates $\{\pi_t\}_t$, while a backward loop sets $\{\gamma_t\}_t$. The smoothing posterior is then simply obtained by multiplying both–see (5).