This blog-post is the first of a short series on the modern algorithmic Reinforcement Learning landscape. The series’ objective is 1) to lay out the borders of some “boxes” where one can fit most modern RL algorithms, 2) define said boxes’ content in an almost self-contained fashion and 3) discuss each algorithmic family’s strengths and weaknesses. This first post provides a very brief description of what those boxes are.

Our discussion starts with the now famous drawing from David Silver’s course:

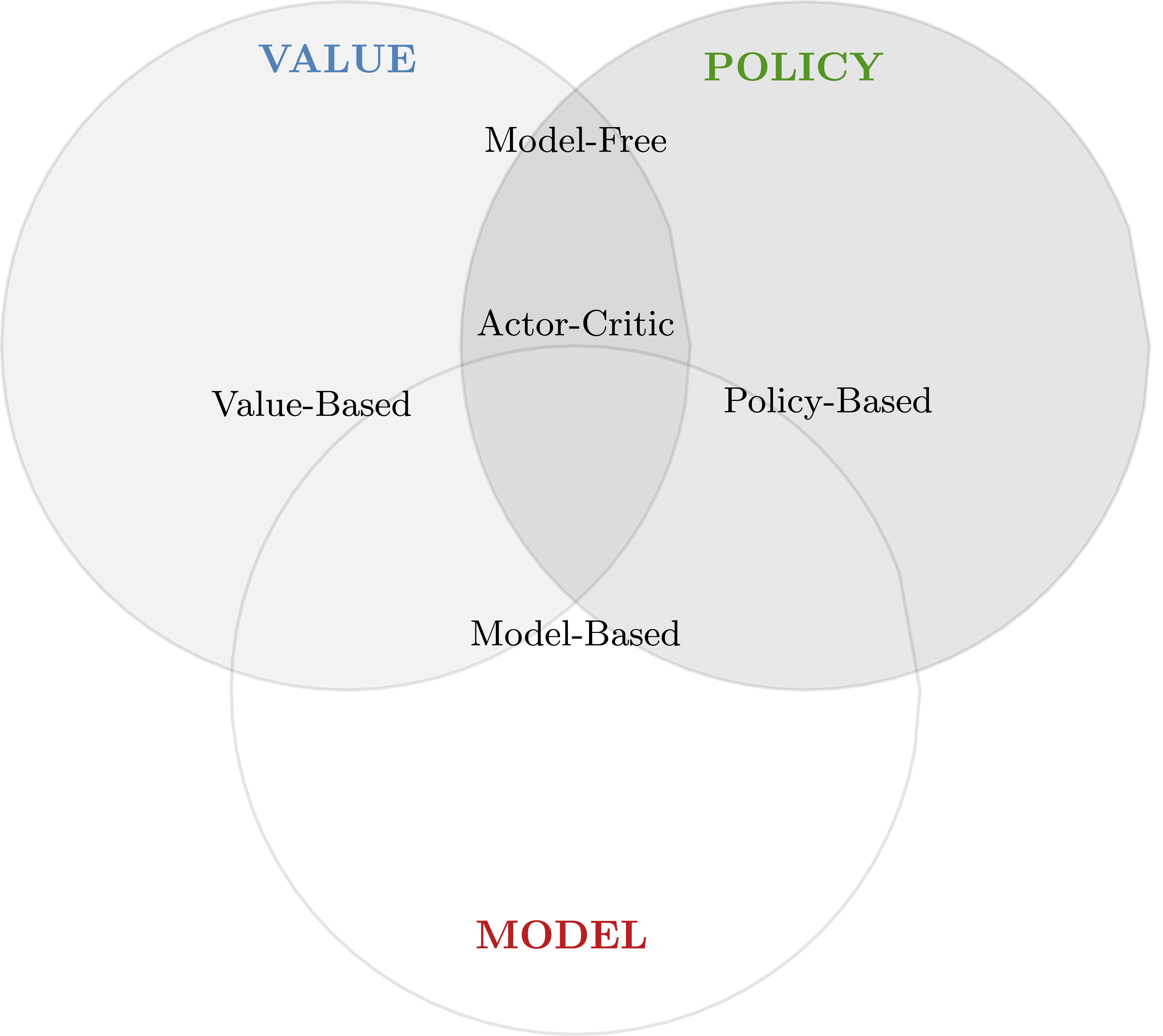
What distinctively differentiates RL algorithms is what they fundamentally try to model. This can be:

• the optimal value-function,
• the optimal policy,
• the unknown MDP generating experience,

or a combination thereof. This yields a myriad of approaches with many moving pieces, making it sometimes hard (in my opinion) to develop a cold classification-based understanding of different techniques. Below, we briefly cover each one of the three algorithmic “boxes”, their origins and overlaps. Future post will dive deeper into each box.

Value-based approaches

The underpinning goal to value-based approach is to approximate correctly the optimal value function $v_\lambda^\star$ – or more precisely, its action-based sibling: $$ q_\lambda^\star(s, a) := \max_{\pi} \mathbb{E}^\pi \Big[\sum_{t\geq 1} \lambda^{t-1} r(s_t, a_t)\vert s_1=s, a_1=a\Big] \;. $$ from which an optimal policy can be easily deduced via $ \pi^\star(\cdot\vert s) \in \argmax_{a\in\mathcal{A}} q_\lambda^\star(s, a) \; . $

Value-based methods are typically off-policy: there is no need to explicitly maintain a policy in charge of collecting experience. Value-based approaches are therefore expected to be sample-efficient – the downside being that they require extra effort to stabilise when coupled with function approximation.

Virtually all value-based approaches are descendants of the Value-Iteration (VI) algorithm. The stochastic approximation of VI is the famous Q-learning algorithm. Its successors (DQN and friends) were designed to support neural networks as function approximators, and the dynamic instabilities they brought with them.

Policy-based approaches

We won’t expand too much on purely policy-based approaches: they have known a limited success in modern RL. This is probably because maintaining only policies throws away the strong structure of RL problems carried by the Bellman equations—itself baked into value-functions. This was, for instance, the idea of the Vanilla Policy Gradient (VPG, see A Tale of Policy Gradients). (There exist other purely policy-based methods, relying e.g. on Evolutionary Algorithms approaches, which we will not cover.)

The VPG was quickly augmented with control variates: baselines under the form of value-functions estimates for the current policy. Algorithms mixing policy optimisation with Bellman-backed value functions are known as actor-critic methods. This sub-branch of RL has been particularly prolific for problems where sample-efficiency is not an issue (e.g. when one can access a cheap simulator). In such settings, actor-critic algorithms have gained the reputation of being rather stable and robust.

Model-based approaches

While model-free methods try to find an optimal solution straight from data, model-based approaches have a more prudent philosophy. Briefly, they first build a model for the world, fit this model from data, and then build control laws for the resulting approximation.

Concretely, model-based approaches attempt to learn transition kernel $p$ and the reward function $r$ of some MDP $\mathcal{M} = (\mathcal{S}, \mathcal{A}, p, r)$ – state and action spaces are assumed known. The idea is somewhat simple; if we have learned a good model for the MDP, then we can apply classical control methods (e.g. value-iteration, linear-quadratic regulator, model predictive control, ..) to find an efficient policy.

Most theory-backed algorithms (i.e algorithms with provable finite-time performance guarantees) are relying on model-based approaches. Of course, most often, said algorithms operate on tabular / small MDPs, and under strong confining assumptions.